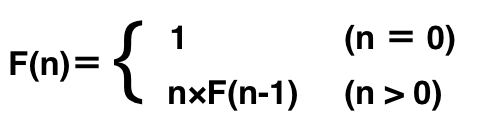【基本情報技術者試験の再帰関数の問題】意外にシンプル！実際のコーディング例も解説します！！

実際に出題された基本情報技術者試験の再帰関数のテーマに関する過去問と解答、解説をしていきます。

大きく以下２つの出題パターンを紹介します。

※if文とは、プログラミングにおける条件分岐構文のこと。

与えられた条件により、処理が分岐されるというものです。

数学が苦手関数！難しい！と悩む方も安心してください。

記事後半では、再帰関数に関する最もシンプルな形を実際のコーディング例で紹介！

理解できるように、基本的なことから解説します。

まずは、平成22年秋期の、基本情報技術者試験に実際に出題された問題を例の紹介し解説します。

1.if文を使わない問題

n!の値を，次の関数F(n)によって計算する。乗算の回数を表す式はどれか。

ア.n－1

イ.n

ウ.n²

エ.n!

出典：基本情報技術者試験　平成24年秋期　問7

答えはイ

それでは解説します。

解説

これは、if文を使っていない問題です。

与えられた条件式（問題文にある図）を読み取り、実際に値を入れながら結果（F(n)）を自分で検証していく必要があります。

ではまず、問題文にある図をみてみましょう。

これは与えられたnの値により、F(n)が異なります。

例を書きます。

となります。

このように、与えられたnの値によりF(n)が変わります。

では次に問題文をみてみましょう。

問題文にある「n!」とは「階乗」のことです。

「階乗」とは、その自然数以下のすべての自然数を掛け合わせた数値のこと。

例を書きます。

３の階乗は３!と書き、

と表されます。

さて、問題は「乗算の回数を表す式はどれか」というもの。

ですから乗算の回数を求めるには、まずは問題文に与えられた式に、実際に値をいれて確認します。

仮に3の階乗「3!」で試してみます。

（n=3は0より大きいため問題文の図の下の条件に当てはめます）

F(3) = 3×F(3 - 1)

= 3×F(2)

ところで、F(2)は以下で表せます。

F(2) = 2×F(2 - 1)

= 2×F(1)

さらに、F(1)は以下で表せます。

F(1) = 1×F(1 - 1)

= 1×F(0)

ここで、F(0)は、問題文（図）より1となります。

F(0) = 1

上記のことから、F(3) は以下のように表せます。

F(3) = 3×F(2)

= 3×2×F(1) ・・・F(2)は2×F(1)

= 3×2×1×F(0) ・・・F(1)は1×F(0)

= 3×2×1×1 ・・・F(0)は1

よって「3×2×1×1」中の「×の回数」は3回。

ですから、3!（3の階乗）の乗算回数は3回ということになります。

解説をみても分かるように、ある関数を処理した結果、さらに同じ関数が書かれています。

例えば、F(3) という関数を実行すると、3×F(2)という結果が返されています。

実はこれ（F(2)）が、再帰関数と呼ばれるもので自分自身（F(n)）を呼び出しています。

以降、F(2) = 2×F(1)、F(1) = 1×F(0)...と繰り返されていき、すべての処理が終わると、最終的な答えが返ってくるのです。

ここでのポイントは以下です。

与えられた式や条件などややこしいとは思います。

ですが、仮に値を決めて一つづつ条件に合致する処理を行うことで、正答が導き出せます。

では次節、「if文を使った問題」を紹介し解説します。

以下は、令和元年秋期に行われた、基本情報技術者試験の過去問となります。

2.if文を使った問題

自然数nに対して，次のように再帰的に定義される関数f(n)を考える。f(5)の値はどれか。

f(n)：if n≦1 then return 1 else return n＋f(n－1)

ア.6

イ.9

ウ.15

エ.25

出典：基本情報技術者試験　令和元年秋期　問11

答えはウ

解説していきます。

解説

いきなりプログラミング形式の出題です。

しかし、不安にならなくても大丈夫。

考え方や解法を解説していきます。

まず与えられた関数をみてみましょう。

何やら英語が並んで、よくわかりません。

この場合、以下のように書き換えてみましょう。

すると、f(n)関数には「if」と「else」という記述が出てきており、条件（「n」の値により）により処理が分かれることに気づきます。

f(n)関数について一つづつ解説します。

1.【if〜】nが1以下の場合を示す条件式

nが1以下の場合を示す条件式です。

例えば、n=1の場合にはこの条件に合致。

合致すると、その下の処理（1を返す）が行われます。

2.【else 〜】nが1より大きい場合を示す条件式

nが1より大きい場合を示す条件式です。

「if n≦1 then」に合致しない場合という風に言い換えることができます。

例えば、n=4の場合にはこの条件に合致。

合致すると、その下の処理（n+f(n-1)を返す）が行われます。

関数に値を入れて検証する

以上、f(n)関数の処理内容を理解したところで、実際に値を入れて検証しましょう。

問題文ではn=5が提示されています。

n=5は、f(n)関数の下部の条件に合致します。

ですので、返される値（return）は、

f(5) = 5 + f(4)

上記式のf(4)関数もf(n)関数の下部の条件に合致します。

ですので、返される値（return）は、

f(4) = 4 + f(3)

以降、同様にf(n)関数の条件に従い検証していきます。

f(3) = 3 + f(2)

f(2) = 2 + f(1)

ここで、f(1)関数は、n=1であるため、f(n)関数の上部の条件に合致します。

そのため、

返される値（return）は、

1

上記をまとめると、以下の５つ式が出来上がります。

f(5) = 5 + f(4)

f(4) = 4 + f(3)

f(3) = 3 + f(2)

f(2) = 2 + f(1)

f(1) = 1

ですから、n=5の場合の値は

f(5) = 5 + 4 + 3 + 2 + 1

となりますから、答えは15となります。

ここでのポイントは以下です。

英語ばかりでややこしい。

しかし、こういったプログラム構文をマスターするには、実際にコーディングしてみることが一番手っ取り早いです。

次節、実際に再帰関数を使ったプログラムをご紹介します。

終盤でコードを書いて実行できますから、ぜひ試してくださいね！

再帰関数を使った実際のコーディング例

ここでは実際にpytonを使って、1からnまでの総和を返す基本的なプログラムを紹介します。

 html
def calc(n):
if n < 1:
return n
return n + calc(n-1)
s = calc(10)
print("計算結果➡︎", s)

このプログラムを実行すると、以下のような結果が得られます。

計算結果➡︎ 55

解説

再帰関数は、以下のとおりたった４行で完結してしまうシンプルなものです。

 html
def calc(n):
if n < 1:
return n
return n + calc(n-1)

nが1未満になると、そのnを返し終了します。

nが1以上だと、以下の結果を返しています。

n + calc(n-1)

例えば、n=2の場合だと、

2 + calc(1)とさらに自分自身を呼び出しています。

次に、再帰関数を呼び出しているところです。

 html
s = calc(10)
print("計算結果➡︎", s)

引数（n）に10を与えています。

結果（s）をprint関数で表示させています。

上記コードを変えながら、除算や乗算などやってみてくださいね。

下記リンクでpythonの実行できますよ！

➡︎オンライン実行環境

実際にコーディングをやってみることで、再帰関数のしくみがよく分かります。

まとめ

基本情報技術者試験の再帰関数の過去問について紹介、解説しました。

再帰関数は基本情報技術者試験だけではなく、ITの開発現場においてもたびたび使用されます。

しかし再帰関数を使う、良し悪しはあります。

ですが、複雑な問題を簡単な問題に置き換えて処理できるというメリットがあるのです。

また、スマートなコーディングだと、誰がみても分かりやすいので保守や改造するにも容易ですからね。

この機会に、再帰関数をしっかりマスターしておきましょう！

人気記事【基本情報技術者試験の過去問（午前）】何年分解けばいい？よく出る問題をランキング形式で紹介し解説！